How Shit Works - Teledildonics
How Shit Works - Teledildonics
Ring Ring Ring Ring Ring Ring BANANAPHONE (Intro)
If the table of contents is confusing you, you must've been living under a non-flash enabled rock when this was going around. That also means you missed the episode of Full House where Michelle gets totally addicted to a Raffi song and plays it until the tape dies! YOU'RE MAKING UNCLE JESSE CRY!
If you are not currently familiar with the work of Raffi, now would be a good time to study up. Our upcoming tutorial on anal electrostimulation will be set to the tune of Baby Beluga, and I expect ALL of you to be singing along.
I've got a feeling, so appealing, for us to get together and ?!?! (About Teledildonics)
So, yeah, Teledildonics: a word as fun to say as "Gazebo"; a word that has been flying around the blogs of every hip, cool person who doesn't blush about sex; a word that has been around for years but still represents hilarious failure.
Here's the definition as provided by Wikipedia: _ Teledildonics (also known as Cyberdildonics) is the integration of telepresence with sex. The term is considered somewhat humorous and speculative but not so much that it cannot be used in serious contexts; indeed it is the only commonly-used word to express the precise concept. In the original conception, this technology could be used for "remote" sex (or, at least, remote mutual masturbation), where the physical sensations of touch could be transmitted over a data link between the participants _
Basically, teledildonics is remote sex. You hit a button, and someone else in a far away place gets all vibratey. In its current form, the implementation is ridiculously simple. No one has done much of anything interesting with teledildonics yet. However much that sucks for the end user, if you're reading this, you're probably not one of them. You're an enterprising hacker who wants to get off using your computer. It's very easy to understand the current state of things in remote controlled sex, and to start improving on them, and that's just what we expect you to do.
It's no baloney, it ain't a phoney (A very short history of teledildonics)
I am not about to recount the history of teledildonics when it has already been so wonderfully done by Violet Blue. Instead, I'll just provide you with links to her writing.
Teledildonics Now, Part One Teledildonics Now, Part Two
One thing not mentioned in those articles: SymToys made the Symphony, which, I'm assuming from the pictures of OS 9, actually predates quite a few of the toys mentioned in that article. Unfortunatly it is no longer produced. They make neat games, though. Mac games at that.
There, now you're all up to date on the commerical side of teledildonics. Ready to put them all out of business?
Cellular, Modular, Interactivodular (Teledildonics protocols and mediums)
Before we go into how the toys talk to each other, we'll cover how toys connect to computers, and what makes those connections different from each other. This part is somewhat optional, as it is not referenced in the rest of the article, but if you're interested about how the commands get from your computer to your toy, you might be interested in this.
To initially talk to a computer, a toy has to connect through one of three types of ports: parallel, serial, or USB. I'm not aware of any firewire, bluetooth, or WiFi toys at this time, but I'm sure they're on their way.

The parallel port. What once was a normal feature on every computer is now going the way of the ISA card and the experience of having to set your own fucking IRQs on your fucking Gravis Ultrasound so you could tweak memory for 3 hours to get the newest Future Crew demo to work.
Good times, good times.
The parallel port on most machines consists of 25 pins (or, if you've got an old printer, there was the Centronics type port, which had one big slot/plug in the middle). 8 of these pins were used for data, which means you could send or receive 1 full byte (8 bits, or 8 0's and 1's) at a time, which made it pretty fast. However, due to the size of the port and difficulty of programming for it, parallel ports started disappearing around the advent of USB, and while still around, are now not considered a standard feature of some motherboards.
Currently, the only toy I know of that uses the parallel port is the Open Dildonics Project, and their site seems to be all but defunct these days.

Next up, the serial port. Like the parallel port, it's been a standard on most computers for years. It is still enjoying a more useful life than the parallel port, as can be seen through the abundance of Serial to USB versus Parallel to USB converters. It's starting to disappear from some of the smaller laptops, though.
The serial port is usually a 9 pin connection. Instead of transmitting 1 byte at a time, the serial port can only transmit 1 bit at a time, which makes it slower than the parallel port. However, programming for the serial port is an easier task, and one that we will be covering in our FreeSex Network articles in the near future.
The VR Innovations toy and Highjoy's Doc Johnsons Modified toys talk through the serial port.
Our final physical connection type is USB, the current leader in connection types for PC's. There's damn good reason for this. From the beginning, USB was designed to a very strict standard. Protocols, physical design, and electronics were all written into the standard. Other ports implement some combination of these, but not enough to make sure that everyone will be using the same connectors when products are shipped from different vendors. This means that if you got a USB device from 3 different vendors, you could at least assume some basic similarities in the products, which would make things easier to work with.
USB is guaranteed to provide a certain amount of power through the port, meaning that if you can create a product that doesn't suck too much juice from the PC, you won't need an extra power supply in order to run the device. In terms of sex toys, which usually require a small amount of power for a motor, this is a huge advantage.
Finally, USB is much, much faster than parallel or serial. At this moment in time, we aren't too interested in speed. Most devices need to receive one, maybe two numbers in order to control the speed of their motors. USB 1.1 gives you 12Mbps, which is much more than we'll need at this point. Once we start encasing video screens in toys, then we might start pushing the connection a little.
The Sinulator and Utopex both use USB connections for their products, though the Sinulator offers an RF wireless connection to go along with their toys.
If you want a good, in depth but still understandable overview of the history and specficiations of USB, I recommend this article on ibm.com.
Now then, you figure that when someone is making sweet hoo-hoo joyfun (6 months into running this site and we're already running out of terms for sex) to a machine, they don't exactly want to be getting up close and personal with a mid-size tower. Wireless toys seems like the optimal solution. As of this writing, there is currently only one wireless toy available, The Sinulator. However, due to the fact that we love being through, and since you might want to build your own remote toy someday, here's a quick overview of how basic wireless connections work right now.
IR, or Infrared Frequency, is what you use to change the channel on your TV, or possibly to transfer data unreliably between your PDA and laptop. It has very low power requirements and the circuitry to control it is simple. Unfortunatly, it requires line of sight between the two points for the connection (meaning if your leg accidently gets in the way, no more vibration control), and it's susceptible to both light and physical barriers. Putting multiple IR emitters in close vicinity can also cause massive interference issues, even if they work on different carrier frequencies. No IR sex toy gangbangs for you!
No sex toys I know of use IR, probably for reasons mentioned above. However, if you're interested in building quick and easy IR projects to control through your PC just for fun, I recommend the USB UIRT.
RF, or Radio Frequency, doesn't suffer nearly as many problems as IR. Line of sight isn't as issue (otherwise you'd never get to listen to your favorite radio station or talk on your cell phone), neither is light or (most) physical objects. All of you faraday cage fetishists are shit out of luck, however.
Developing for RF is a little more difficult than IR, due to the fact that RF is regulated by the FCC. If you want to produce a commerical product using RF in the US, you must register it with the FCC in order to sell it to the public. This step make sure you aren't going to be stepping on the toes of any other product (at least, that's the nice way of putting it, but FCC hate is a whole other story...).
The Sinulator uses an RF connection with its USB key to communicate wirelessly.
Bluetooth is a current favorite for small devices, but has a high implementation cost, varying range, and somewhat flakey connection status due to the bonding mechanism it uses. You'll see Bluetooth used in cellphones, for wireless keyboards/mice, and in some PDAs, but it's still a fairly underused technology at the moment. No toys use it.
The Wireless USB standard was recently passed (May 2005), but it will be at least a few months before we see any products on the market that use it, and possibly up to a year before any sex toys come out with this standard. It promises the same speeds as USB 1.1 with up to 10 feet of wireless range, which is just fucking AWESOME for the teledildonics community. Converters will be available to turn any current USB 1.1 device into a USB Wireless device. It's gonna totally r00l.
So, that's a few of the possible ways you could connect a sex toy to your computer or other electronic device. Onto the software interface.
Ping Pong Ping Pong Ping Pong Ping PANANAPHONE (How the software works)
Teledildonics software isn't exactly Mathematica. At the core, all you need is a network connection, and something that allows the user to enter a power level for the remote toy. Let's take a look at a few of the software interfaces currently available for toys, and how they fit into this description.
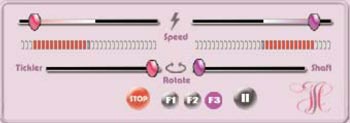
The Highjoy Control GUI. Understated, quiet, pink, boring. This is like having sex with a feminine hygiene product commerical. This version of the HJ GUI is for the rabbit vibrator, so you've got two different types of control, speed and rotation direction, for both the rabbit tickler and the shaft. Of course, it's damn near impossible to tell which direction is faster/slower, and which rotation side is clockwise/counter-clockwise. It also has a stop and pause button.
So, that fulfills the basics of the controls we set out at the beginning of this section, and doesn't do much else interesting.

The Sinulator runs as far as it can on the other side of the unsexy GUI spectrum. It's well known that everyone gets off better when they think they're flying a spaceship with a gigantic penis in the middle of the dashboard. As with the HJ GUI, it fulfills the simple purpose of being able to send some sort of speed settings to the remote end. It just looks like they hired an 8 year old to design it.
Then there's Utopex. I love Utopex, they make my life so easy, 'cause I don't even have to try to make fun of them. It's just so bad...



Wow, rip off many ideas lately?
So it's obvious that they picked up the spaceship idea from the Sinulator kids. I seriously fucking hope they plan on replacing the horrible cartoons with video though, otherwise I might feel even more cheated out of the $400 for their toys.
Ok, so obviously I have nothing to say about usage of the Utopex GUI that hasn't already been said. I just bought myself a family sized case of hateraid today, and I'm chuggin' like Bo Jackson after a game of Tecmo Bowl.
If you can dig through the accidental UI design critique this has become, you can see how simple these interfaces are. For all the fluff and graphics around them, none of them are really all that usable, especially for the skant functionality they control. They are simply a gussied up version of this:
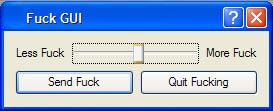
Now, there's all sorts of things you can add to make your teledildonics experience more human. Chat clients, video streams.... Well, ok, so those are the only things that have been added so far. No reason in going over them, as they're just icing on the cake.
We will skip marrily past how the everything below the GUI works. Networking is a wonderfully interesting topic, however it will be throughly covered in our FreeSex tutorials, as it will bore to tears anyone who's just here to read about how to make things vibrate over long distance.
Nonetheless, here's a quick overview of what happens on both sides of the connection with the GUI. The pitching end of the connection uses these GUIs to send the control information to the catching end of the connection. The catching end receives the commands, and forwards them to whatever connection port (USB, serial, etc...) is being used. The on-toy processing then figures out what that command means, and readjusts accordingly, which is what we'll cover next.
It's the best, beats the rest (How the hardware works)
Now we're down to the hardware, the iron, the big steel. That's right, the part that makes this tutorial worth it.
Note: The method we present here covers implementation for things that vibrate, or move at some sort of variable speed. This isn't the only way to implement remote sex toys, nor do we know if it's the way that any commerical toys actually work. However, this is us giving it a good ol' college try. We've made projects using this method, so we can guarantee that it works for us, and it should work for you, too.
First off, if you haven't read our hastily cobbled together tutorial about how vibrators work, and you aren't familiar with the basics of electricity and DC motors, I recommend you check it out. It can be accessed by clicking here.
In the normal, human controlled use of a vibrator, the user has some sort of switch or knob that they lets them control the functions (speed/intensity) of the vibrator. The aim to teledildonics is to transfer this control onto a computer. Now, unless you want to build a little robotic hand to turn the knob for you, the whole switch/knob situation isn't going to work. So, how are we going to control the speed without physical access to the vibrator control? By using a method called Pulse Width Modulation, or PWM.
First off, let's get familiar with the new hardware we're adding to the vibrator mix. The main chip in this circuit is the motor driver. Although USB (and parallel, if you don't care about blowing fuses) provides enough power to turn a small vibration motor, serial does not. We're therefore stuck with the power from the data signals sent through serial or USB. These don't have NEARLY enough power to turn a motor. A small motor can require anywhere between 100-500mA. Data signals run at roughly 10-20x less. So we need a chip that can take a data signal, and use that to "flip a switch" that's connected to a decent power supply in order to run the motor. That's basically what a motor driver is. You set a power supply (in this case, 2-3 AA batteries depending on what we're powering) through the motor driver, hook your data line up to it, and every time the data line transmits a 1 (or "goes high", as 1's just refer to a certain steady voltage being carried over the line for a certain amount of time), the power is switched on to the motor. Motor drivers also provide filtering and h-bridge support, but that's a lesson for another tutorial.
Now we know how to turn the switch on and off using the computer, but how does that makes the motor go faster and slower? Well, remember, electricity is fast. Really fast. Like, way totally fast. Really. That switch can be turned on and off thousands of times per second. If the switch isn't on all the time, only a certain portion of the total amount of electricity can get to the motor in order to power it. The motor only goes as fast as the amount of power it's getting.
Here's a quick and simple way to test this idea in your own home (This is, of course, assuming your lighting system runs off of DC, which it probably doesn't):
- Screw a perfect lightbulb (one that has zero rise/falloff time) into the socket in your room.
- Make sure no one that is easily susceptible to seizures is in the room.
- Go over to the light switch, and try to attain a 60hz switching rate. This means you'll need to flip the switch on and off 60 times per second, and perfect intervals of 1/60th of a second. Come on, you've played video games for years, man the fuck up and DO IT.
- Now, go down to a 30hz rate, or flipping the switch on and off 30 times per second. See how the room is roughly half as lit as it once was?
Putting this back in terms of teledildonics, let's say the pitcher sends a 50% PWM request over the line. Once the catcher receives that command, the motor driver will be commanded to send power for 50% of every time cycle, so only 50% of the power reaches the motor, and it only goes (theorically, assuming linear rampup) half as fast as it possibly could.
Here's what a 50% PWM looks like:
_ _ _ _ _ _ _ _ | | | | | | | | | | | | | | | | Clock | | | | | | | | | | | | | | | | __| |____| |____| |____| |____| |____| |____| |____| |____ ______ ______ ______ ______ <--- up means power is on power | | | | | | | | | | | | | | | | __| |______| |______| |______| |______ Versus 100% PWM: _ _ _ _ _ _ _ _ | | | | | | | | | | | | | | | | Clock | | | | | | | | | | | | | | | | __| |____| |____| |____| |____| |____| |____| |____| |____ _______________________________________________________ Power | | __|
If you'd like to learn more about PWM, check out the Wikipedia article that I stole the text graphics from!
That's it! Now you've got enough knowledge to build your own computer controlled sex toy! Go, create, and remember me when you make your millions!
My Cellular Bananular Phooooooooooooooone (Wrapup)
See? Teledildonics is easy! All it takes is a little sweat, elbow grease, and minimum of a bachelors degree in 3 engineering fields! Soon you'll be on your way to paying some bastard licensing fees in order to be able to market your product! Aren't patents fun?
Anyways, that's it for our technical overview of all things teledildo. Come back next time for... whatever the hell it is we do next.

